5.3. ЗАДАЧА НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ОГРАНИЧЕНИЯХ НЕРАВЕНСТВАХ
Теорема Куна-Таккера. Рассмотрим случай задачи с ограничениями-неравенствами :
минимизировать 
(5.3.1)
при ограничениях
(5.3.2)
В точке минимума 
неравенства 
могут выполняться как равенства или строгие неравенства.
Ограничение называется активным в точке , если оно выполняется в ней как строгое равенство, то есть если 
Используя геометрические свойства допустимой области, найдем необходимые условия экстремума для задач минимизаци с ограничениями. Для этого сначала рассмотрим случай, когда все линейны. Итак, пусть требуется найти 
при условии
(5.3.3)
Здесь каждое ограничение (5.3.3) определяет полупространство в 
. Допустимая область 
задана пересечением 
полупространств, определяемых неравенствами (5.3.3), и следовательно, является выпуклым многогранником. Вектор 
является нормалью к гиперплоскости, определяемой уравнением 
, и направлен внутрь области .
Пусть точка является точкой минимума задачи (5.3.1) с ограничениями (5.3.3). Обозначим множество индексов активных ограничений через
(5.3.4)
Например, на рис.5.9 приведен пример минимизации с линейными ограничениями при 
. Выберем любую допустимую точку 
из . Вектор 
направлен из внутрь области . Такой вектор будем называть входящим. Для этого вектора с учетом того, что 
, можно записать следующее условие:
,
или
(5.3.5)
для всех 
и 
.
 |
Таким образом, входящий вектор
определяет допустимое направление перемещения из точки . Но так как минимальна в точке , то при любом , удовлетворяющем (5.3.5) , будем иметь:
(5.3.6)
Применим теперь теорему, которая есть следствием леммы Фаркаша (см. приложение 1). Из условий (5.3.5), (5.3.6) на основании леммы Фаркаша следует, что существует множество неотрицательных скаляров 
, для которых
(5.3.9)
Отметим, що уравнение (5.3.9) аналогично (5.2.15). Если принять , что 
при 
(то есть для неактивных ограничений), (5.3.7) можно переписать в виде
(5.3.10)
Кроме того, получим, что
(5.3.11)
поскольку при 
, а при 
. Поэтому уравнения ограничений можно включить в целевую функцию следующим образом:
(5.3.12)
Следовательно, удовлетворяет следующим условиям:
(5.3.13)
(5.3.14)
При рассмотрении задачи минимизаци при условиях 
может случиться так , что не будет существовать таких 
, для которых без дополнительных предположений о природе функций были бы справедливы уравнения (5.3.13), (5.3.14), где - оптимальное решение. Эти дополнительные предположения называют условиями регулярности ограничений. В частности, в рассмотренном случае, в качестве таких условий использовали линейную независимость векторов-градиентов ограничений 
.
Теорема Куна-Таккера. Выше найдены условия оптимальности (5.3.11), (5.3.12) для задачи НП с линейными ограничениями. Обобщим эти условия на случай задачи (5.3.1), (5.3.2), когда все ограничения нелинейны.
Условия оптимальности решения задачи НП формулируются в следующей теореме, имеющей исключительно важное значение в теории нелинейного программирования [2; 18].
Теорема 5.8 (Куна-Таккера). Пусть функции 
, имеют непрерывные частные производные на некотором открытом множестве , содержащем точку . Если является точкой минимума функции при ограничениях 
, удовлетворяющих условию регулярности в виде линейной независимости векторов 
, то существуют такие неотрицательные множители Лагранжа 
, что
(5.3.15)
(5.3.16)
Определим функцию Лагранжа следующим образом:
(5.3.17)
Тогда теорему Куна-Таккера можно записать в виде
(5.3.18)
(5.3.19)
(5.3.20)
Заметим, що множители Лагранжа 
в задаче НП с ограничениями-равенствами являются знаконеопределенными, тогда как в теореме Куна-Таккера они должны быть положительными.
Доказательство. При достаточно малых 
, разлагая 
в ряд Тейлора, получим
(5.3.21)
где 
- остаточный член второго порядка малости 
. Пусть
- множество активных ограничений. Тогда
так как 
при . Заметим, що система неравенств
|
несовместна, так как в противном случае при достаточно малом для некоторого 
получили бы:
что противоречит предположению об оптимальности точки . Для дальнейшего доказательства воспользуемся леммой, являющейся следствием леммы Фаркаша (см. приложение 1).
Лемма. При произвольной матрице 
выполняется одно из двух условий:
либо выполняется следующая система неравенств:
(5.3.24)
либо выполняется следующая система равенств (уравнений):
(5.3.25)
Одновременно условия (5.3.24), (5.3.25) выполняться не могут.
Применим эту лемму к (5.3.22), (5.3.23), приняв за матрицу
Поскольку система (5.3.22), (5.3.23) не имеет решений, то существуют такие 
что
(5.3.26)
где 
Если присвоим значение 0 для 
, то получим 
. Условие называют условием дополняющей нежесткости.
Покажем, что 
в (5.3.26) не может равняться 0. В самом деле, если допустить, что 
, то получим
(5.3.27)
Однако (5.3.27) противоречит условию теоремы о линейной независимости векторов . Остается принять 
. Тогда, разделив обе части (5.3.26) на , получим
Следовательно, теорема доказана.
Понятие регулярности было впервые введено Г.Куном и А.Таккером и имеет различные формы. В частном случае, когда и все 
являются выпуклыми функциями, условие регулярности записывается в виде: существует такой вектор , что 
для всех 
. Это означает, що может существовать хотя бы одна внутренняя точка допустимого множества решений. Это условие называют условием регулярности Слейтера [2; 3].
Седловая точка и задача нелинейного программирования
Рассмотрим функцию Лагранжа
Определение 5.7. Пара векторов 
называется седловой точкой функции Лагранжа 
, если при всех 
выполняется условие
(5.3.28)
Неравенство (5.3.28) называют неравенством для седловой точки. Очевидно, что в седловой точке выполняется условие
(5.3.29)
Между понятием седловой точки функции Лагранжа 
и решением задачи НП существует взаимосвязь, которая устанавливается в следующей теореме.
Теорема 5.9. Пусть и все выпуклы и функции удовлетворяют условию регулярности Слейтера. Вектор является решением задачи НП (5.3.1), (5.3.2) тогда и только тогда, когда существует такой вектор 
, что
(5.3.30)
и
(5.3.31)
Доказательство. Сначала докажем достаточность условий теоремы. Пусть 
- седловая точка функции . Тогда из правого неравенства (5.3.26) получим
(5.3.32)
Поскольку 
, а , то 
. Вместе с тем 
согласно с (5.3.31). Поэтому из (5.3.30) следует неравенство
для всех , удовлетворяющих ограничениям задачи НП. Таким образом, 
- оптимальное решение задачи НП.
Перейдем к доказательству необходимости. Допустим, что -оптимальное решение задачи НП. Заметим, что система
(5.3.33)
не имеет решения, так как - точка минимума задачи НП. Отсюда следует также, что не имеет решений и следующая система:
(5.3.34)
Тогда согласно теореме Фана существуют такие 
что
(5.3.35)
Поскольку
то
для всех . (5.3.36)
Если же в (5.3.35) положить 
, то получим
(5.3.37)
Сравнив (5.3.36) с (5.3.37), получим
(5.3.38)
Тогда из уравнений (5.3.35) и (5.3.38) получим
(5.3.39)
Таким образом доказано правое неравенство для седловой точки. Поскольку 
, то 
при любом 
. Следовательно,
(5.3.40)
Разделив обе части (5.3.40) на 
, получим левое неравенство для седловой точки:
Таким образом, теорема доказана.
Чтобы обеспечить условие , необходимо предположить существования условия регулярности Слейтера. В самом деле, пусть 
. Тогда выражение (5.3.39) пимет вид
(5.3.41)
Вместе с тем условие регулярности Слейтера утверждает, что существует такой вектор , что 
, и, следовательно, 
. Так как это противоречит уравнению (5.3.41), то предположения теоремы вместе с условием регулярности Слейтера обеспечивает ее справедливость.
Таким образом, при выполнении условий теоремы 5.9 задача НП становится эквивалентной задаче отыскания седловой точки функции Лагранжа.
Применение теоремы Куна-Таккера
для задачи выпуклого программирования
Више была рассмотрена задача НП в виде (5.3.1), (5.3.2), когда на переменные 
не накладывались условия неотрицательности. Тем не менее часто в задачах исследования операций приходится решать задачи, в которых переменные по физическим условиям должны удовлетворять условию
для всех 
.
Покажем, как основные положения изложенной теории можно распространить и на этот случай. Действительно, пусть задача НП имеет вид:
минимизировать (5.3.42)
при ограничениях
(5.3.43)
(5.3.44)
Введем обозначения 
. Тогда ограничения (5.3.44) можно записать в общем виде:
(5.3.45)
Теперь задача задана в каноническом виде (5.3.1), (5.3.2). Применим к ней теорему Куна-Таккера, для чего составим функцию Лагранжа:
(5.3.46)
где 
- множители, связанные с ограничениями 
. Условия теоремы Куна-Таккера для (5.3.46) выглядят так:
или
(5.3.47)
(5.3.48)
(5.3.49)
Условия (5.3.47), (5.3.48), (5.3.49) можно записать в следующей эквивалентной форме:
(5.3.50)
(5.3.51)
Нетрудно увидеть, что условия (5.3.51) представляют собой условия дополняющей нежесткости для ограничений неотрицательности.
Таким образом, найдены необходимые условия для оптимального решения задачи НП вида (5.3.42) - (5.3.44), которые можно сформулировать в следующей теореме [18].
Теорема 5.10. Пусть задача НП задана в виде (5.3.42) - (5.3.44), а функции и 
дифференцируемы и выпуклы (по x). Вектор 
является оптимальным решением задачи НП тогда и только тогда, когда существует такой вектор 
, что пара 
является седловой точкой функции Лагранжа, то есть выполняются такие условия :
(5.3.52)
(5.3.53)
(5.3.54)
. (5.3.55)
Задача (5.3.42) - (5.3.44) при условиях, что все 
- выпуклые функции, является задачей выпуклого программирования. Ограничения , определяют выпуклое множество, и требуется найти минимум выпуклой функции на выпуклом множестве решений 
. Рассмотрим задачу вогнутого программирования.
максимизировать (5.3.56)
при ограничениях
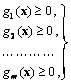(5.3.57)
(5.3.58)
где и все функции вогнуты по .
Покажем ее эквивалентность задаче выпуклого программирования (5.3.42) - (5.3.44). Для этого обозначим 
, и так как max f ~ min - f(x), то приходим к задаче:
минимизировать 
(5.3.59)
при ограничениях
(5.3.60)
(5.3.61)
Легко увидеть, что все функции 
будут выпуклы по , а поэтому задача (5.3.59) - (5.3.61) - это задача выпуклого программирования. Итак, эквивалентность задач (5.3.56) - (5.3.58) и (5.3.42) - (5.3.44) установлена.
Нетрудно получить соответствующие признаки оптимальности для задачи (5.3.56) - (5.3.58), аналогичные условиям (5.3.52) - (5.3.55).
Теорема 5.11. Пусть задача НП задана в виде (5.3.56) - (5.3.58), а функции 
, - дифференцируемы . Для того чтобы вектор 
являлся оптимальным решением этой задачи, необходимо, чтобы существовал такой вектор , для которого выполнялись бы такие условия:
а) 
(5.3.62)
б) (5.3.63)
в) 
(5.3.64)
г) 
(5.3.65)
Если функции 
вогнуты, то условия (5.3.62) - (5.3.65) оказываются и достаточными.
