6.10. ПОЛИНОМИАЛЬНЫЙ АЛГОРИТМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим новый алгоритм ЛП, предложенный Н. Кармаркаром в 1984 г. Он имеет полиномиальную сложность. Этот алгоритм в идейном плане близок к алгоритму эллипсоидов и применяется к задачам ЛП, приведенным к некоторой специальной форме.
Постановка задачи
Рассмотрим задачу ЛП над рациональными числами, которая приведена к такой канонической форме:
минимизировать 
(6.10.1)
при ограничениях
, (6.10.2)
, (6.10.3)
где 
. (6.10.4)
Пусть 
означает подпространство 
, а 
означает симплекс 
. Обозначим через 
пересечение 
Тогда рассмотренная проблема будет иметь вид:
минимизировать (6.10.5)
при ограничениях 
.
Оптимизация на сфере
Если заменим ограничение 
на ограничение вида 
, где 
- сфера, то нетрудно заметить, что оптимальное решение можно найти, решая линейную систему уравнений.
Сечением сферы и афинного пространства является сфера меньшего размера внутри этого афинного пространства.
Откуда задача становится следующей:
минимизировать 
при ограничениях ,
где с' - получена ортогональным проектированием с на . Эта задача тривиальная. Из центра сферы необходимо сделать шаг в направлении -с', длина которого равна радиусу сферы.
Границы целевой функции
Пусть 
- строго внутренняя точка множества 
. Допустим, что мы построили эллипсоид 
с центром , который содержится в , и решаем оптимизационную задачу на ограниченной области вместо . Чтобы найти границы целевой функции, построим второй эллипсоид 
, увеличивая на достаточно большой коэффициент 
, так чтобы содержал в себе . Тогда 
, где 
. Обозначим через 
минимальные значения ц.ф. 
на множествах , и соответственно. Тогда 
, откуда
.
Последнее неравенство следует из линейности 
:
, (6.10.6)
или
. (6.10.7)
Таким образом, перейдя из точки в точку 
, минимизирующую на , приближаемся к минимальному значению с коэффициентом 
. Далее можно повторить тот же самый процесс, используя в качестве центра новой сферы (эллипсоида).
Как видим, скорость сходимости этого метода зависит от : чем меньше , тем быстрее сходится метод.
Проективные преобразования
Рассмотрим проективные преобразования пространства 
, описываемые формулой вида
, (6.10.8)
где 
и матрица 
невырожденная.
Нас интересуют проективные преобразования гиперплоскости 
Эти преобразования описываются следующим образом:
, (6.10.9)
где 
- невырожденная матрица. Для каждой точки 
многогранника 
, где 
существует единственное проективное преобразование 
гиперплоскости 
, которое фиксирует все вершины и перемещает точку 
в центр 
.
Эти преобразования задаются выражением
. (6.10.10)
Сравнив (6.11.10) с (6.11.9), увидим, что соответствующая матрица 
является диагональной
. (6.10.11)
Преобразование имеет следующие свойства:
- однозначное преобразование, отображающее симплекс в себя.
Обратное преобразование задается следующим образом:
. (6.10.12)
Каждая грань симплекса, задаваемая 
, отображается в соответствующую грань 
Образ точки 
является центром симплекса, задаваемого точкой 
.
Пусть 
означает 
-й столбец матрицы 
. Тогда система уравнений
превращается в систему
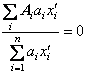(6.10.13)
или 
, где 
.
Будем обозначать афинное подпространство 
через 
. Если 
, то центр симплекса 
. Пусть 
- наибольшая сфера радиуса 
с центром , совпадающим с центром симплекса, которая содержится в симплексе , т.е. вписанная в него. Аналогично, пусть 
- наименьшая сфера (т.е. наименьшего радиуса 
), содержащая в себе симплекс . Нетрудно показать, что 
и кроме того,
.
Очевидно 
. Но 
- это образ многогранника 
.
Сечением сферы и афинного подпространства является сфера меньшего размера в том же самом подпространстве, и она имеет тот же самый радиус, если центр исходной сферы лежит в афинном подпространстве. Отсюда мы получим выражение
;
которое доказывает, что размерность пространства 
можно всегда получить этим методом.
Инвариантные потенциальные функции
Алгоритм генерирует последовательность точек 
, имеющие убывающие значения ц.ф. . На 
-м шаге точка переводится в центр симплекса с помощью проективного преобразования. Далее мы оптимизируем ц.ф. на сечении вписанной сферы и афинного подпространства, чтобы найти следующую точку 
. Основываясь на результатах предыдущих разделов, можно надеяться, что целевая функция будет уменьшена хотя бы в 
раз на каждом шаге.
Тем не менее здесь мы сталкиваемся со следующим явлением. Множество линейных функций не инвариантно относительно проективного преобразования, тем не менее отношение линейных функций преобразовывается в отношение линейных функций. С каждой линейной ц.ф. 
свяжем потенциальную функцию 
вида
,
где - некоторая константа.
Эта функция имеет следующие свойства:
любого произвольного уменьшения в значении можно достичь уменьшением значения ;
отображается в функцию той же самой формы с помощью преобразования (трансформации) , рассмотренного выше;
оптимизации на каждом шаге можно достичь приближенно путем оптимизации линейной функции.
Описание базового алгоритма
Чтобы сосредоточиться на главных идеях, сделаем некоторые упрощающие допущения. В разделе 3 мы их снимем и покажем, как привести общую задачу линейного программирования (ЗЛП) к канонической форме.
Итак, пусть задача ЛП задана в канонической форме (6.10.1)-(6.10.4). Сделаем следующие допущения:
для всех 
,
допустимая начальная точка, т.е. 
, причем 
.
Результаты работы алгоритма следующие: либо существует 
такое, что 
, либо делается вывод, что 
.
Алгоритм задает последовательность точек 
вследствие выполнения следующих шагов (здесь шаги обозначены буквой Ш).
Ш.0. Задать 
- центр симплекса (многогранника).
Ш.1. Вычислить следующую точку последовательности: 
.
Ш.2. Проверить допустимость.
Ш.3. Проверить оптимальность: если условие (признак) оптимальности не выполняется, то перейти к первому шагу.
Дадим теперь подробное описание алгоритма.
Первый шаг. Он имеет вид 
и состоит из следующих процедур, которые будем обозначать П.
П 1. Проектирующее преобразование симплекса , отображающее входную точку в центр .
П 2. Приближенная оптимизация преобразованной целевой функции на вписанной сфере для нахождения 
.
П 3. Применение обратного преобразования 
в точке , чтобы получить исходную точку 
.
Опишем подробно основные процедуры.
П 1. Проектирующее преобразование 
.
Пусть 
, а 
- диагональная матрица. Тогда задается так:
,
где 
.
Зададим матрицу 
, т.е. прибавим к матрице строку 
.
Приближенная оптимизация на сфере (алгоритм А).
Свяжем ц.ф. с потенциальной функцией вида
.
Пусть 
- преобразованная потенциальная функция, которая определяется как 
. Тогда
,
где 
.
Пусть - преобразованное афинное пространство . Тогда 
. Таким образом, - нуль-пространство.
П 2. Оптимизация насфере
Пусть 
- радиус наибольшей сферы с центром , который можно вписать в симплекс . Тогда 
. Будем оптимизировать 
на сфере меньшего размера по двум причинам: 1) это позволит оптимизацией функции очень близко аппроксимировать оптимизацией линейной функции; 2) если будем выполнять арифметические операции приближенно, а не точно (в классе рациональных чисел) то это позволит получать такие погрешности округления, которые не выведут за границы симплекса.
Ограничим афинное пространство 
с помощью уравнения 
. Пусть 
- результирующее афинное пространство, и обозначим 
. Тогда любой сдвиг в является сдвигом в нуль-пространстве. Нас интересует оптимизация на множестве 
.
Заменим минимизацию потенциальной функции на минимизацию линейной функции на сфере. Рассмотрим алгоритм оптимизации на вписанной сфере 
.
Спроектировать вектор 
ортогонально на нуль пространство 
:
. (6.10.14)
Нормализовать 
.
Сделать шаг длиной 
в направлении 
и вычислить
, (6.10.15)
где 
- параметр, который можно взять равным ¼.
Применив к обратное проектирующее преобразование (процедура П З), получим вектор
. (6.10.16)
Использовать в алгоритме в качестве новой исходной точки.
Второй шаг. Проверка допустимости. Ждем улучшения на величину 
потенциальной функции
на каждом шаге. Значение параметра зависит от выбора параметра 
на первом шаге. Например, если 
, то 
. Если нет ожидаемого улучшения, т.е. 
, то останавливаемся и делаем вывод, что минимальное значение целевой функции строго больше 0. Эта ситуация соответсвует случаю, когда начальная задача не имеет конечного оптимального решения при условии, что каноническая форма получена преобразованием стандартной ЗЛП.
Третий шаг. Проверка оптимальности. Эта проверка делается периодически. Она включает переход из текущей внутренней точки в крайнюю точку без увеличения значения ц.ф. и проверки этой крайней точки на оптимальность. Эта проверка делается только тогда, когда пройдет заданное время с момента последней проверки.
Теоретическое обоснавание алгоритма
Приведем несколько теорем, которые дают теоретическое обоснование полиномиального алгоритма Кармаркара.
Сначала докажем существование точки, обеспечивающей постоянное уменьшение потенциальной функции. Это утверждается в следующей теореме.
Теорема 6.7. Существует точка 
такая, что 
, где - некоторая константа.
Далее докажем, что минимизацию можно аппроксимировать (заменить) минимизацией линейной функции.
Теорема 6.8. Пусть - точка, минимизирующая на . Тогда 
, где - положительная константа, зависящая от . Для можно положить . Наконец рассмотрим алгоритм А оптимизации на сфере . Он обосновывается следующей теоремой.
Теорема 6.9. Точка , которая вычисляется в алгоритме А, минимизирует на .
Завершают теоретическое обоснование алгоритма следующие теоремы о сходимости метода.
Теорема 6.10. За 
шагов алгоритм находит допустимую точку, такую что
. (6.10.17)
Теорема 6.11. При использовании алгоритма выполняется одно из двух условий:
,
где - некоторая константа, которая зависит от значения параметра первого шага;
минимальное значение ц.ф. строго положительно.
Докажем эти теоремы.
Доказательство теоремы 6.7. Пусть 
- любая точка такая, что 
,
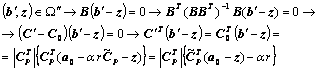(6.10.18)
, так как
(6.10.19)
Следовательно, 
, для всех 
.
Пусть 
- точка в 
, где достигается минимум . Очевидно, что 
. Пусть - точка, в которой линейный отрезок 
пересекает границу сферы 
для некоторого 
. По определению 
и 
. Из этого следует, что 
. Откуда
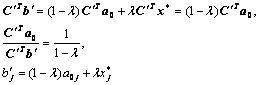(6.10.20)
Откуда
. (6.10.21)
Далее используем следующее неравенство. Если 
, то 
. Поэтому
(6.10.22)
, (6.10.23)
где - радиус наименьшей описанной сферы, 
,
, (6.10.24)
,
. (6.11.25)
Выбрав 
, получим . Итак, теорема 6.7 доказана.
Доказательство теоремы 6.8. Сначала рассмотрим несколько вспомогательных лемм.
Лемма 6.5. Если 
, то 
.
Доказательство этой леммы основано на простых результатах математического анализа.
Лемма 6.6. Пусть 
. Тогда для любого 
. (6.10.26)
Доказательство. Из того, что , следует 
. Поэтому 
. Далее 
для всех 
В соответствии с леммой 6.5.
Доказательство. Из того, что , следует 
. Поэтому . Далее для всех
Согласно лемме 6.5.
(6.10.27)
Здесь 
. (6.10.28)
И подставив (6.10.28) в (6.10.27), получим окончательно
. (6.10.29)
Теперь докажем теорему 6.8.
Обозначим 
. Пусть 
- точка в 
, в которой достигает минимума.
Справедлива следующая цепочка равенств
Согласно теореме 6.7
(6.1.30)
Для 
.
Согласно лемме 6.6
, (6.10.31)
Поскольку 
монотонно возрастающая функция от , то и достигают своего минимального значения на 
в одной и той же точке (а именно в)
:
Согласно (6.10.30) - (6.10.32)
.
Положим
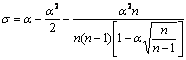. (6.10.33)
Тогда
. (6.10.34)
Заметим, что:
. Если 
, то 
,
если 
, то 
.
Доказательство теоремы 6.9. Согласно теореме 6.7. Применив обратное преобразование 
и подставив 
, получим 
Доказательство теоремы 6.10. Для любого
(6.10.35)
(6.10.36)
Однако 
. Следовательно, 
. Поэтому существует константа 
такая, что после 
шагов
. (6.10.37)
Приведение общей задачи ЛП к каноническому виду
Рассмотрим задачу ЛП в стандартной форме:
минимизировать 
(6.10.38)
при ограничениях
, (6.10.39)
. (6.10.40)
Покажем, как эту задачу можно привести к требуемому каноническому виду (6.10.1)-(6.10.2). Этот переход основывается на теории двойственности.
Первый шаг. Рассмотрим двойственную задачу к (6.10.38)-(6.10.40):
максимизировать 
(6.10.41)
при ограничениях
,
. (6.10.42)
Объединим прямую и двойственную задачи в одну:
; (6.10.43)
; (6.10.44)
Согласно теории двойственности эта комбинированная задача допустима тогда и только тогда, когда исходная задача (6.10.38) имеет окончательное решение.
Второй шаг. Введем свободные переменные 
и получим
(6.10.46)
Третий шаг. Введем искусственную (фиктивную) переменную 
, чтобы получить внутреннюю допустимую начальную точку:
минимизировать (6.10.47)
при ограничениях
(6.10.48)
Заметим, что 
- строго внутреннее допустимое решение, которое можно выбрать в качестве начальной (стартовой) точки. Минимальное значение 
равно 0 тогда и только тогда, когда задача на втором шаге допустима.
Для удобства дальнейшего описания сделаем замену обозначений и запишем задачу на третьем шаге в виде
минимизировать 
при ограничениях
,
где 
- известная строго внутренняя стартовая точка и предельное значение ц.ф., которое нас интересует, равно 0.
Четвертый шаг. Выполним проективное преобразование положительного ортанта в симплекс.
Рассмотрим преобразование 
, где 
определены в соответствии с
, (6.10.49)
.
Пусть 
означает положительный ортант , 
- симплекс 
Преобразование 
обладает следующими свойствами:
отображает в ;
оно однозначное, а обратное к нему задается следующим образом:
; (6.10.50)
образом точки является центр симплекса;
пусть - это -й столбец матрицы . Если 
, то
, или 
.
Итак, определили столбцы матрицы 
с помощью следующих уравнений:
Тогда 
. (6.10.51)
Пусть означает афинное подпространство, т.е. 
. Таким образом, имеем систему однородных уравнений в пространстве ;
поскольку мы заинтересованы в получении значения ц.ф., равном 0, определим 
как афинное подпространство, которому соответствуют следующие значения ц.ф.:
.
Подставив сюда
,
получим
.
Определим 
при условиях
Тогда из 
следует 
. Итак, образ задается как 
. Таким образом, преобразованная задача имеет вид
минимизировать 
(6.10.52)
при ограничениях
; (6.10.53)
; (6.10.54)
. (6.10.55)
Центром симплекса является допустимая начальная точка. Таким образом, исходная задача (6.10.38)-(6.10.40) приведена к канонической форме.
Применение базового алгоритма А к этой задаче либо даст решение 
такое, что 
, либо приходим к выводу, что минимальное значение 
строго больше 0. В первом случае обратное отображение в 
даст оптимальное решение исходной задачи. Во втором случае исходная задача не имеет конечного оптимума, т.е. она либо неразрешима, либо ц.ф. не ограничена.
Вычислительная сложность алгоритма
Значение ц.ф. уменьшается с постоянным коэффициентом для всех 
шагов. Определим:
, (6.10.56)
где 
- квадратная подматрица матрицы ограничений,
. (6.10.57)
Ясно, что величина 
не больше, чем длина входной последовательности. В процессе работы алгоритма периодически контролируем оптимальность, преобразуя решение с внутренней точкой в решение с внешней точкой без ухудшения значения ц.ф. и проверяем оптимальность крайней точки.
Два любых различных значения ц.ф. на вершинах должны различаться по крайней мере в 
для некоторой константы 
. Поэтому максимум на 
шагах достигаем в ситуации, в которой любая крайняя точка лучше, чем текущая внутренняя точка.
На каждом шаге необходимо решать линейную систему уравнений, которая требует 
арифметических операций. Тем не менее, если будем решать уравнения на каждом шаге, изменяя (модифицируя) решение предыдущего шага, то можем уменьшить количество операций благодаря множителю 
(этот метод описан в приложении 4).
Для каждой арифметической операции нужна точность 
бит. Отметим, что эта точность необходима для любого метода, решающего уравнение 
, если 
.
Множитель вида может появиться при оценивании сложности любого алгоритма ЛП, поскольку представление выхода может требовать бит на одну переменную (в наихудшем случае).
Заключительный анализ и выводы
Метод Кармаркара и алгоритмы, которые базируются на нем, могут оказаться полезными при разработке алгоритмов со свойствами глобальной сходимости. Этот метод можно рассматривать как метод наискорейшего спуска в некотором специальном метрическом пространстве на симплексе. Глобальные свойства полученных результатов стали возможными благодаря тому, что произвольную строго внутреннюю точку можно отобразить в любую другую внутреннюю точку с помощью преобразования, которое сохраняет афинность пространства и его метрику. Эту метрику легко обобщить на произвольные выпуклые множества с 'хорошими' границами, а также на сечение этих множеств. Эта метрика эффективно преобразует допустимую область так, что границы области будут находиться на бесконечном расстоянии от внутренних точек.
Более того, это преобразование не зависит от вида ц.ф., которая оптимизируется.
Поскольку представление исходных переменных в задаче ЛП требует в наихудшем случае двоичных разрядов на одну переменную, то параметр может появиться в оценке сложности произвольного алгоритма ЛП. На практике намного меньше 
. Поэтому там, где можно заменить множитель на , необходимо это сделать, если есть заинтересованность в получении алгоритма, эффективного на практике.
Функционирование алгоритма на практике
Каждый шаг алгоритма требует оптимизации линейной функции на эллипсоиде или, что эквивалентно, решения системы линейных уравнений типа 
, где - фиксированная матрица, а 
- диагональная матрица с положительными элементами, которая медленно изменяется на каждом шаге.
Разработанный метод базируется на последовательных модификациях ранга 1. Для него доказано, что верхняя граница необходимого числа операций на один шаг составляет 
(смотри приложение 4).
На практике встречаются разреженные матрицы. Поэтому можно сконструировать более эффективные методы для решения рассмотренной выше проблемы. Еще одна особенность алгоритма, которая может привести к сокращению вычислений, следует из того, что не обязательно нужно искать строго оптимальное решение.
Полезно различать два вида приближенных решений. Пусть 
- точное, а - приближенное решение.
Будем отличать сильное приближение (или приближение в пространстве решений) от слабого приближения (или приближение в пространстве целевых функций).
Сильное приближение требует, чтобы решение было близким к в некоторой метрике, а слабое - чтобы было близким к 
.
Для предложенного метода вполне достаточно слабого приближения, а его легче достичь численными методами.
Число шагов зависит от 
. Мы показали, что это отношение имеет верхнюю границу . Однако достоверно, что оно будет меньше в некоторых типичных практических задачах. Возможность улучшения отношения порождает целый ряд проблем, требующих дальнейшего анализа, таких, например, как вероятностный анализ проблемы, анализ специальных интересных с точки зрения практики случаев задач, как, например, задачи с ограничением типа параллелепипедов, а также поиск лучшей оценки для верхней границы вычислений.
Вычислительная стойкость и погрешности округления
В предложенном алгоритме погрешности округления не накапливаются. Наоборот, этот алгоритм самокорригируется в том понимании, что погрешность округления, полученная на первом шаге, компенсируется на следующих шагах. Если допущена погрешность в 1% в вычислении вектора 
на каждом шаге, то можно компенсировать погрешности, увеличивая число шагов прогона алгоритма на 2%.
